Inferencia estadística univariada

Fecha de publicación

5 de julio de 2024

Presentación

Objetivo de la práctica

El objetivo de esta guía práctica es aplicar los conocimientos aprendidos en clases sobre inferencia estadística univariada, comprendiendo sus fundamentos, relevancia y aplicación a un caso concreto en R.

En detalle, aprenderemos:

  1. Establecer el diseño muestral de una base de datos en R.

  2. Realizar estimaciones puntuales e intervalares para medias y proporciones.

  3. Contrastar hipótesis univariadas.

Recursos de la práctica

En esta práctica trabajaremos con la base de datos de la Encuesta Suplementaria de Ingresos (ESI) del 2021 realizada por el Instituto Nacional de Estadísticas (INE). Esta base la pueden encontrar en el canal de U-Cursos sección Material Docente, o bien, en el siguiente enlace ESI 2021 podrán descargar el archivo que contiene la base ESI 2021.

¿Qué es la inferencia estadística?

Recordemos que, en estadística, llamamos inferencia al ejercicio de extrapolar determinadas estimaciones (estadístico) de una muestra a una población más grande (parámetro). En concreto, es el proceso de realizar conclusiones o predicciones sobre una población a partir de una muestra o subconjunto de esa población.

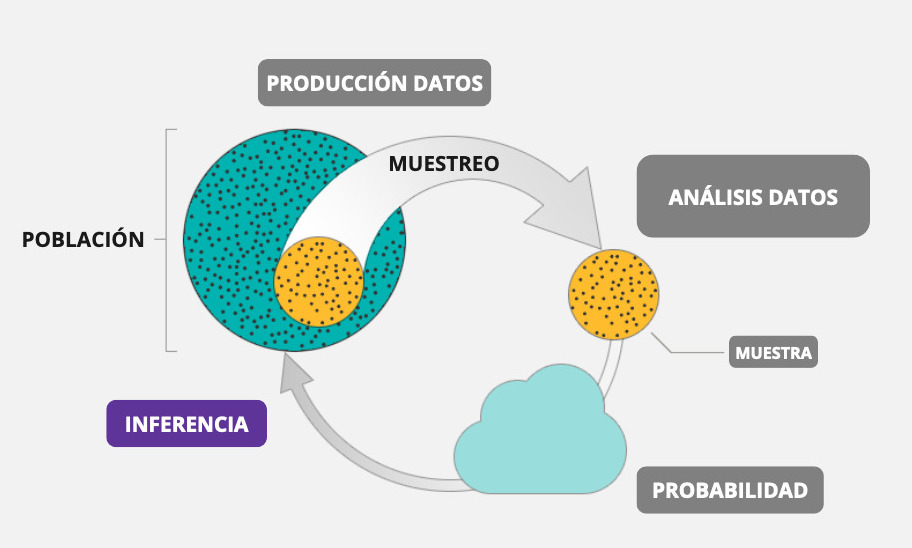
Un concepto central en todo esto es la probabilidad de error, es decir, en qué medida nos estamos equivocando (o estamos dispuestos a estar equivocados) en tratar de extrapolar una estimación muestral a la población.

Preparación de datos

1. Cargar librerías

Para esta sesión, usaremos librerías que ya conocemos en prácticos pasados y una nueva, llamada srvyr:

pacman::p_load(tidyverse, # colección de paquetes para manipulación de datos
               car, # para recodificar
               psych, # para analizar datos
               sjmisc,  # para analizar datos
               srvyr) # para estimación de IC y ponderadores

options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo

2. Importar datos

Cargamos la base de datos ESI 2021 con readRDS

esi <- readRDS("Input/data/esi-2021-ocupados.RData")

3. Recodificar

Solo recodificamos y convertiremos a factor la variable sexo.

esi$sexo <- car::recode(esi$sexo, recodes = c(" 1 = 'Hombre'; 2 = 'Mujer'"), as.factor = T)

Declarar diseño muestral

Como sabemos, las encuestas se basan en procedimientos de muestreos, los cuales debemos declarar para poder realizar el ejercicio de inferencia, o dicho de otra manera, debemos indicar el procedimiento mediante el cual podremos extrapolar nuestras estimaciones a la población.

Por tanto, antes de poder realizar inferencia, debemos tener muy claro el tipo de diseño muestral de nuestra base de datos.

Con srvyr, como primer paso debemos identificar dos variables para poder establecer el diseño muestral en una base de datos:

  • la variable de diseño muestral que incorpora efectos de diseño complejo y,
  • el ponderador o factor de expansión.

Todo este diseño se contiene en variables de la base de datos. Veamos todas las variables que son parte del diseño muestral de la ESI 2021:

   idrph id_identificacion   conglomerado estrato fact_cal_esi
1  14565            102542      820510025 8200111    253.12888
2  24946             69274 13123000144956   13291    238.89778
3  89327             63472      610110021 6100112    161.60639
4 116589             52414  5301000042099    5031     46.40046
5 122766             73953   100691030131   10069     21.67297
6 210896             88382      210110141 2100011    181.86029

En el caso de la ESI 2021, la variable que indica el efecto del diseño muestral se llama estrato y la que indica el factor de expansión o ponderador es fact_cal_esi.

Ahora, el segundo paso es crear un objeto survey con estas variables:

esi_pond <- esi %>% as_survey_design(ids = 1, # indica conglomerados de muestreo; ~0 o ~1 cuando no hay
                                     strata = estrato, # indica efecto de diseño muestral
                                     weights = fact_cal_esi) # indica el ponderador

options(survey.lonely.psu = "certainty") # seteamos para que ids no moleste

Ahora tenemos una base ponderada además de la original. Esta base ponderada reconoce el diseño muestral y nos permitirá realizar estimaciones que se acerquen al paramétro poblacional.

Estimaciones de punto y de intervalo

Todo estimador está compuesto por dos elementos:

  • Estimación puntual
  • Precisión (por ejemplo, Intervalos de Confianza “IC”)

Perfectamente podemos conocer el valor que obtiene un estadístico a nivel de la población mediante la estimación puntual, pero esto nada nos dice del nivel de certeza o precisión de dicho cálculo. Aquí es donde entran los Intervalos de Confianza (IC).

Los IC nos indican un rango de valores que pueden contener el valor poblacional o parámetro desconocido, con un determinado nivel de confianza. Piensa en un IC como una red: es un rango de valores posibles para los parámetros de la población, y podemos tener un X% de confianza (normalmente el 95%) en que la red recoge el parámetro de la población.

Dado que normalmente conocemos valores solo de nuestra muestra, nuestra estimación tendrá cierto grado de incertudumbre. Un IC aborda esta incertidumbre proporcionando un rango de valores dentro del cual creemos que es probable que se encuentre el verdadero parámetro de la población.

Importante: cuando se habla de intervalos de confianza, en realidad no se puede decir nada sobre la estimación del parámetro propiamente tal, sino que nos referimos a la red o al rango en sí.

Se puede decir legalmente lo siguiente

Con un 95% de confianza se puede sostener que este intervalo de confianza capta el verdadero parámetro de población

El nivel de confianza refiere al grado de certeza que tenemos de que el parámetro estará contenido en el intervalo que hemos estimado. Por ejemplo, al decir “con un 95% de confianza”, significa que en un 95% de las muestras los intervalos obtenidos comprenderán al verdadero parámetro.

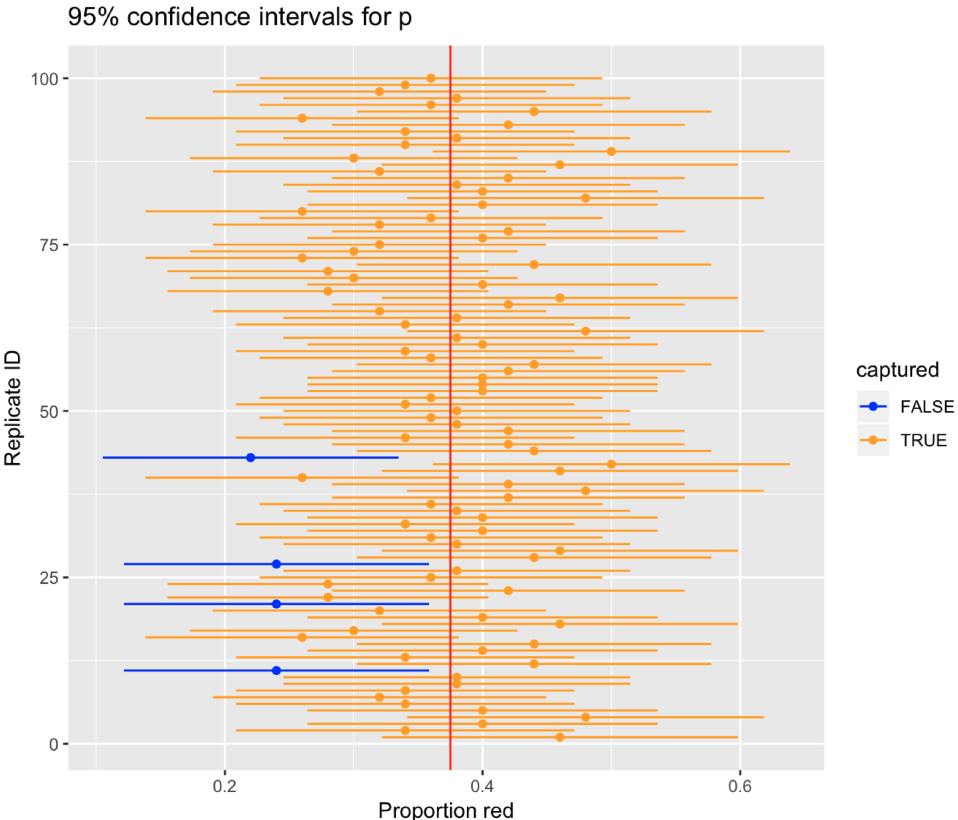
En este práctico realizaremos inferencia sobre dos estimaciones: 1) el ingreso promedio del trabajo de las personas ocupadas y 2) la proporción de hombres y mujeres ocupadas, ambos en Chile en el año 2021.

!MANOS A LA OBRA!

a) IC para medias con diseño muestral

Según el informe de resultados de la ESI 2021, el ingreso medio mensual estimado para la población ocupada en Chile fue de $681.039.

Veamos primero el ingreso medio mensual en nuestra muestra o base de datos:

psych::describe(esi$ing_t_p)
   vars     n     mean       sd   median  trimmed      mad min      max
X1    1 37124 586360.4 697362.9 405347.7 474473.1 255411.6   0 38206253
      range skew kurtosis      se
X1 38206253   12   402.32 3619.36

Como podemos apreciar, en nuestra muestra el valor promedio del ingreso mensual de las personas ocupadas fue igual a $586.360, por lo cual ya sabemos que se encuentra lejos del parámetro. En inferencia, más que el valor promedio de una variable en la muestra, nos interesa saber en qué medida ese promedio da cuenta del promedio de la población.

Veamos cómo realizar un IC que considere también la estimación puntual pero que sea extrapolable a la población.

La fórmula de IC para medias es:

\[[\overline{x} - z_{a/2}*\frac{sd}{\sqrt{n}} , \overline{x} + z_{a/2}*\frac{sd}{\sqrt{n}}]\] Pero R hace este cálculo por nosotros, aunque es importante entender la lógica que hay detrás. Ahora, estimemos el IC para el ingreso medio de la población ocupada:

esi_pond %>% 
  summarise(media = survey_mean(ing_t_p, vartype = "ci", levels = 0.95, na.rm=TRUE)) # usamos funcion survey_mean
# A tibble: 1 × 3
    media media_low media_upp
    <dbl>     <dbl>     <dbl>
1 681039.   666563.   695516.

Con este resultado, podemos sostenter que:

  • el ingreso medio mensual de la población ocupada en Chile al 2021 alcanzó los $681.039 y,
  • con un 95% de confianza, este parámetro estará comprendido entre los 666.563 pesos y 695.516 pesos.

b) IC para proporciones con diseño muestral

Según el informe mencionado, en el año 2021, la composición de la población ocupada a nivel nacional se distribuyó de la siguiente manera: aproximadamente el 58% corresponde a hombres y el 42% a mujeres.

La fórmula de IC para proporciones es:

\[[\overline{p} - z_{a/2}*\sqrt{\frac{p*(1-\overline{p})}{n}} , \overline{p} + z_{a/2}*\sqrt{\frac{p*(1-\overline{p})}{n}}]\]

Veamos primero las frecuencias en nuestra muestra o base de datos:

sjmisc::frq(esi$sexo)
x <categorical> 
# total N=37124 valid N=37124 mean=1.44 sd=0.50

Value  |     N | Raw % | Valid % | Cum. %
-----------------------------------------
Hombre | 20806 | 56.04 |   56.04 |  56.04
Mujer  | 16318 | 43.96 |   43.96 | 100.00
<NA>   |     0 |  0.00 |    <NA> |   <NA>

A nivel muestral, los datos parecieran no alejarse del parámetro. Sin embargo, de todas maneras esto no nos permite realizar inferencia y mucho menos asignar algún grado de probabilidad de acierto (o error) a nuestras estimaciones.

Ahora, estimemos el IC para la proporción de hombres y mujeres ocupadas:

esi_pond %>% 
  group_by(sexo) %>% # agrupamos por sexo
  summarise(prop = survey_prop(vartype = "ci", levels = 0.95, na.rm = TRUE))
# A tibble: 2 × 4
  sexo    prop prop_low prop_upp
  <fct>  <dbl>    <dbl>    <dbl>
1 Hombre 0.582    0.575    0.590
2 Mujer  0.418    0.410    0.425

Con estos resultados podemos concluir que, con un 95% de confianza, la proporción de hombres ocupados a nivel nacional se encuentra entre el 57% y el 59%, mientras que el de las mujeres entre el 41% y el 43%.

c) Varios a la vez

Podemos combinar en un solo código gran parte de la información que necesitamos. Además, podemos complejizar el análisis comparando los valores poblaciones entre grupos. Veamos algunos ejemplos:

esi_pond %>% 
  group_by(sexo) %>% 
  summarise(fr = survey_prop(vartype = "ci", levels = 0.95, na.rm = TRUE),
            fa = survey_total(vartype = "ci", levels = 0.95, na.rm = TRUE),
            n = unweighted(n()))
# A tibble: 2 × 8
  sexo      fr fr_low fr_upp       fa   fa_low   fa_upp     n
  <fct>  <dbl>  <dbl>  <dbl>    <dbl>    <dbl>    <dbl> <int>
1 Hombre 0.582  0.575  0.590 4801422. 4727453. 4875391. 20806
2 Mujer  0.418  0.410  0.425 3442157. 3381288. 3503026. 16318

Aquí tenemos tanto la cantidad (fa) como la proporción (fr) de ocupados según sexo. ¿Y si quisiera saber, por ejemplo, el valor promedio del ingreso mensual entre hombres y mujeres?

esi_pond %>% 
  group_by(sexo) %>% 
  summarise(media = survey_mean(ing_t_p, vartype = "ci", levels = 0.95, na.rm = TRUE))
# A tibble: 2 × 4
  sexo     media media_low media_upp
  <fct>    <dbl>     <dbl>     <dbl>
1 Hombre 749046.   726663.   771428.
2 Mujer  586178.   569330.   603026.

Ahora conocemos el valor puntual y sus IC del ingreso mensual de la población ocupada, según sexo.

Contraste de hipótesis

En estadística descriptiva univarada, el contraste de hipótesis se refire a poner a prueba el valor propuesto/hipotetizado de un parámetro.

Sabemos que:

\(H_{0} : \mu\) = valor parámetro (la hipótesis que usualmente queremos rechazar)

\(H_{a} : \mu\) ≠ valor parámetro → \(\mu\) > valor parámetro o \(\mu\) < valor parámetro (la hipotesis que se deriva de nuestra investigación y es complementaria o diferente a la nula)

Los IC son, a su vez, una prueba de hipótesis implícita. Esto nos lleva a interpretar la confianza y el error como dos caras de una moneda. La confianza nos indica con cuanto grado de certeza podemos afirmar que el IC contendrá el parámetro, o bien, la probabilidad de error que esperamos que exista.

Si esto lo llevamos a nuestro ejemplo, podemos plantear que el ingreso medio de la población ocupada será mayor a 600.000. Formalmente sería:

\(H_{0} : \mu\) = 600.000

\(H_{a} : \mu\) ≠ 600.000 → \(\mu\) > 600.000

esi_pond %>% 
  summarise(media = survey_mean(ing_t_p, vartype = "ci", levels = 0.95, na.rm=TRUE)) # usamos funcion survey_mean
# A tibble: 1 × 3
    media media_low media_upp
    <dbl>     <dbl>     <dbl>
1 681039.   666563.   695516.

Con este resultado podemos afirmar que la media de la variable es 681,039 con un IC del 95% que oscila entre 666,563 y 695,516, por lo que la \(H_{0}\) debe ser rechazada (o bien, la \(H_{a}\) recibe apoyo).

Resumen

Hoy aprendimos a realizar inferencia estádistica en R. En detalle, vimos:

  1. Establecer el diseño muestral de una base de datos en R.

  2. Realizar estimaciones puntuales e intervalares para medias y proporciones.

  3. Contrastar hipótesis univariadas.