install.packages("pacman") #para instalar
library(pacman) # para llamar/cargarPráctica 4 Estadística descriptiva
Metodología I - Magíster en Ciencias Sociales
Presentación
Objetivo de la práctica
El objetivo de esta guía práctica es conocer las principales formas de realizar analísis estadísticos descriptivo en R, aplicando los concocimientos aprendidos durante el curso.
En detalle, aprenderemos:
Establecer un flujo de trabajo ordenado en un script (.R).
Aplicar análisis estadísticos descriptivos a variables según su nivel de medición
Recursos de la práctica
En esta práctica trabajeremos con los datos procesados que obtuvimos en la práctica anterior a partir de los datos del Estudio Latinobarómetro.
Flujo de trabajo reproducible
Por temas de orden y reproducibilidad, en este curso vamos a separar en dos momentos el trabajo con datos, y dos archivos de código correspondientes:
Preparación: corresponde a lo que se conoce generalmente como “limpieza”, es decir, realizar las modificaciones necesarias a los datos para poder efectuar los análisis. Estas modificaciones previas al análisis son necesarias ya que los datos originales con los que se va a trabajar en general no vienen perfectamente adaptados a los análisis que se quieren hacer. Por lo tanto, en cuanto a datos también hacemos la distinción entre datos originales y datos preparados (o procesados).
Análisis: se relaciona con análisis estadísticos, en este caso descriptivos, asociados a las preguntas e hipótesis de investigación.
Los procesos de preparación y análisis vinculados tanto a datos y resultados se presentan en el siguiente esquema:
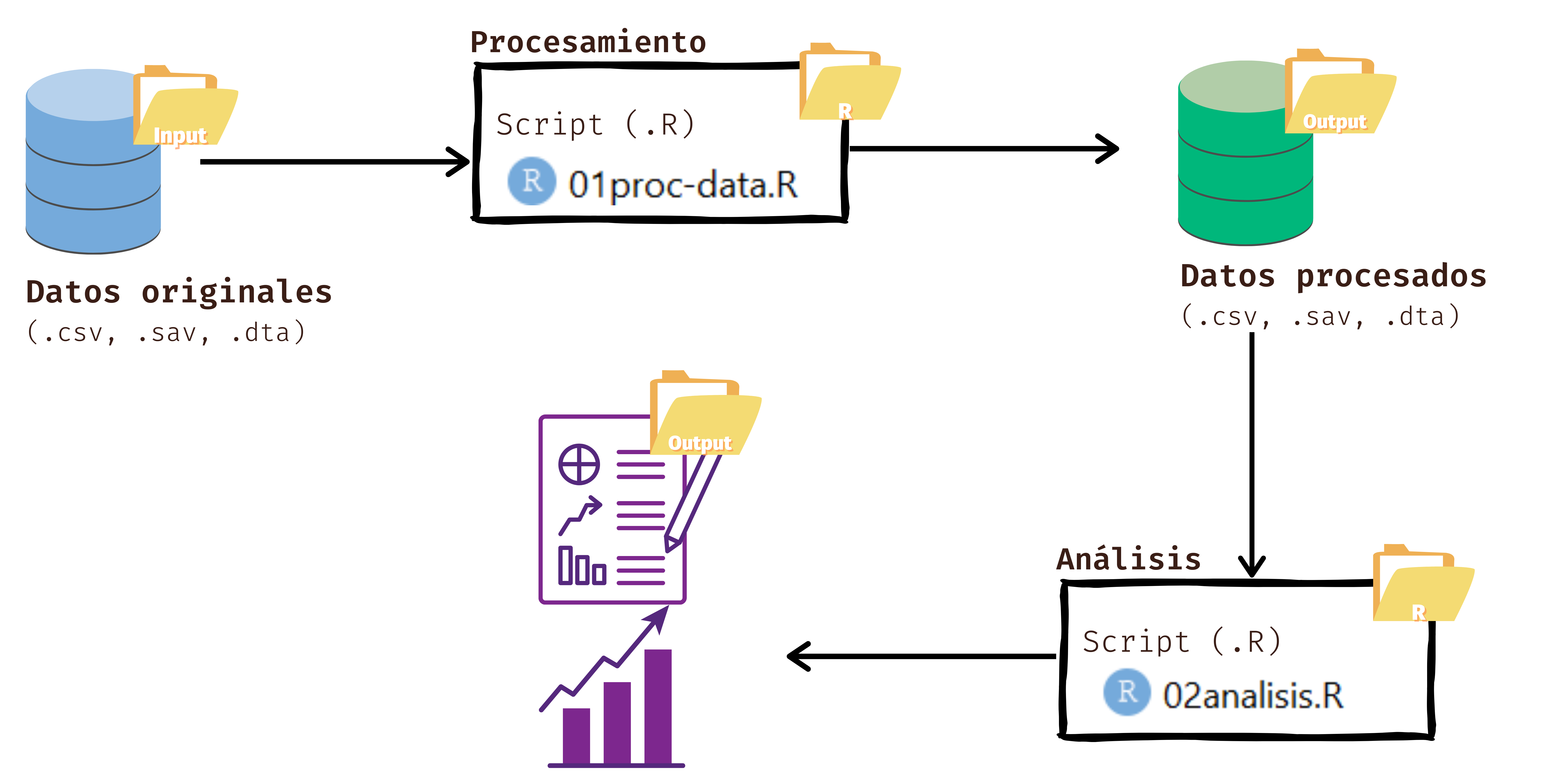
Tanto la preparación como el análisis (que son parte del concepto más general de procesamiento) quedan registrados cada uno en un archivo de código respectivo.
En esta guía nos centraremos en el análisis de datos con R. El documento de código de análisis tiene, por lo menos, 4 partes más una sección de identificación inicial:
- Identificación y descripción general: Título, autor(es), fecha, información breve sobre el contenido del documento
- Librerías: instalar/cargar librerías a utilizar
- Datos: carga de datos
- Explorar: explorar datos
- Análisis: analizar datos y realizar estimaciones
Análisis descriptivo de datos
1 Cargar librerías
Este paso ya lo realizamos y cargamos todas las librerías necesarias. Pero si, al trabajar los distintos script lo hacemos en sesiones diferentes, debemos volver a cargar las librerías.
En este práctico utilizaremos los siguientes paquetes:
pacman: este facilita y agiliza la lectura de los paquetes a utilizar en Rtidyverse: colección de paquetes, de la cual utilizaremos dplyr y havendplyr: nos permite seleccionar variables de un set de datospsych: para analizar descriptivamente datossjmisc: para analizar descriptivamente datossjPlot: para tablas cruzadas o de contingencia
pacman::p_load(tidyverse, # colección de paquetes para manipulación de datos
dplyr, # para manipular datos
psych, # para analizar datos
sjmisc, # para analizar datos
sjPlot) # para tablas de contingencia
options(scipen = 999) # para desactivar notacion cientifica
rm(list = ls()) # para limpiar el entorno de trabajo2 Importar datos
Usamos los datos creados en el procesamiento que se encuentran guardados en la carpeta output.
load("input/data/proc/data_proc.Rdata")o desde internet si no completamos el práctico anterior:
load(url("https://github.com/cursos-metodos-facso/metod1-MCS/raw/refs/heads/main/files/data/latinobarometro_proc.RData"))3 Explorar datos
View(proc_data) # Ver datos
names(proc_data) # Nombre de columnas
dim(proc_data) # Dimensiones
str(proc_data) # Estructura de los datos (las clases y categorias de repuesta)En este caso, nuestra base de datos procesada tiene 1200 casos y 9 variables.
4 Análisis
4.1 Estadísticos descriptivos para variables categóricas
Cuando tenemos variables catégoricas, sean nominales u ordinales, podemos utilizar tablas de frecuencias. Recordemos que las frecuencias es una manera ordenar datos según el valor alcanzado en la distribución de una variable.
4.1.1 Frecuencias
a) Absolutas y relativas
Para las variables nominales podemos usar tablas de frecuencias absolutas y relativas, y con ellas conocer la moda, es dedir, el valor con mayor cantidad de observaciones. Para ello, una manera sencilla de hacerlo es mediante la función table de R.
table(proc_data$sexo)
Hombre Mujer
555 645 table(proc_data$educacion)
Educacion basica Educacion media Educacion superior
97 804 299 table(proc_data$conf_gob)
0 1 2 3
624 358 176 23 Lo anterior nos entrega la frecuencia absoluta de las variables. Con ello, podemos observar que, en cuanto la preferencias entre autoritarismo y democracia, la mayoría de nuestros casos se concentran en “La democracia es preferible a cualquier otra forma de gobierno”. Para conocer la frecuencia relativa o porcentual de estas podemos utilizar el comando prop.table.
(freq_table1 <-table(proc_data$conf_gob))
0 1 2 3
624 358 176 23 prop.table(freq_table1)*100
0 1 2 3
52.836579 30.313294 14.902625 1.947502 Así, podemos sostener que un 52,8% de los casos no confían nada en el congreso.
b) Acumuladas
Mientras que si trabajamos con variables ordinales, podemos usar también la frecuencia acumulada:
(freq_table2 <- table(proc_data$conf_gob))
0 1 2 3
624 358 176 23 (freq_table3 <- prop.table(freq_table2)*100)
0 1 2 3
52.836579 30.313294 14.902625 1.947502 cumsum(freq_table3) 0 1 2 3
52.83658 83.14987 98.05250 100.00000 A partir de este estadístico, podemos ver que un 83,1% de los casos se ubican debajo de la categoría ‘1’ de confianza, lo cual en términos sustantivos señala que un 83,1% de las observaciones confían nada o poco en el congreso.
También podemos unir todas estas frecuencias en una sola tabla:
tbl3 <- table(proc_data$conf_gob)
cbind(Freq=tbl3, relat = prop.table(tbl3)*100, Cum = cumsum(prop.table(tbl3)*100)) Freq relat Cum
0 624 52.836579 52.83658
1 358 30.313294 83.14987
2 176 14.902625 98.05250
3 23 1.947502 100.00000Otra manera de calcular frecuencias (absolutas, relativas y acumuladas) en R, es mediante la función frq() del paquete sjmisc, el cual entrega todo lo anterior con un solo comando.
sjmisc::frq(proc_data$conf_gob)Confianza: Gobierno (x) <numeric>
# total N=1200 valid N=1181 mean=0.66 sd=0.80
Value | Label | N | Raw % | Valid % | Cum. %
------------------------------------------------
0 | Ninguna | 624 | 52.00 | 52.84 | 52.84
1 | Poca | 358 | 29.83 | 30.31 | 83.15
2 | Algo | 176 | 14.67 | 14.90 | 98.05
3 | Mucha | 23 | 1.92 | 1.95 | 100.00
<NA> | <NA> | 19 | 1.58 | <NA> | <NA>4.1.2 Tablas de contingencia
También podemos cruzar dos variables mediante las llamadas tablas de contingencia o tablas cruzadas. Además de conocer la frecuencia absoluta en cada casilla, podemos también conocer la proporción o frecuencia relativa para cada casilla y el total de la filas y columnas.
sjt.xtab(proc_data$sexo, proc_data$conf_gob)| Sexo | Confianza: Gobierno | Total | |||
|---|---|---|---|---|---|
| Ninguna | Poca | Algo | Mucha | ||
| Hombre | 280 | 167 | 93 | 9 | 549 |
| Mujer | 344 | 191 | 83 | 14 | 632 |
| Total | 624 | 358 | 176 | 23 | 1181 |
| χ2=4.015 · df=3 · Cramer's V=0.058 · p=0.260 | |||||
sjt.xtab(proc_data$sexo, proc_data$conf_gob,
show.row.prc = TRUE, #solo fila
show.summary = FALSE) | Sexo | Confianza: Gobierno | Total | |||
| Ninguna | Poca | Algo | Mucha | ||
| Hombre | 280 51 % |
167 30.4 % |
93 16.9 % |
9 1.6 % |
549 100 % |
| Mujer | 344 54.4 % |
191 30.2 % |
83 13.1 % |
14 2.2 % |
632 100 % |
| Total | 624 52.8 % |
358 30.3 % |
176 14.9 % |
23 1.9 % |
1181 100 % |
sjt.xtab(proc_data$sexo, proc_data$conf_gob,
show.col.prc=TRUE, #solo columna
show.summary=FALSE) | Sexo | Confianza: Gobierno | Total | |||
| Ninguna | Poca | Algo | Mucha | ||
| Hombre | 280 44.9 % |
167 46.6 % |
93 52.8 % |
9 39.1 % |
549 46.5 % |
| Mujer | 344 55.1 % |
191 53.4 % |
83 47.2 % |
14 60.9 % |
632 53.5 % |
| Total | 624 100 % |
358 100 % |
176 100 % |
23 100 % |
1181 100 % |
sjt.xtab(proc_data$sexo, proc_data$conf_gob,
show.cell.prc = TRUE, #fila y columna
show.summary = FALSE) | Sexo | Confianza: Gobierno | Total | |||
| Ninguna | Poca | Algo | Mucha | ||
| Hombre | 280 23.7 % |
167 14.1 % |
93 7.9 % |
9 0.8 % |
549 46.5 % |
| Mujer | 344 29.1 % |
191 16.2 % |
83 7 % |
14 1.2 % |
632 53.5 % |
| Total | 624 52.8 % |
358 30.3 % |
176 14.9 % |
23 1.9 % |
1181 100 % |
4.2 Estadísticos descriptivos para variables númericas
A diferencia de las variables categóricas, a las variables numéricas (intervalaras o de razón) les podemos calcular una mayor cantidad de estadísticos descriptivos, como medidas de tendencia central, dispersión o posición.
Como ya vimos en clases:
- dentro de las medidas de tendencia central que podemos calcular para describir a una variable numérica encontramos: media, mediana;
- dentro de las medidas de dispersión podemos señalar: desviación estándar, varianza, coeficiente de variación, rango;
- dentro de las medidas de posición podemos mencionar: mediana, q1, q3, mínimo, máximo.
Recordemos que:
las medidas de tendencia central expresan el valor alrededor del cual se sitúa la mayor cantidad de los datos. Estamos mirando hacia el centro de los datos.
las medidas de dispersión buscan cuantificar lo próximo o alejado que están los valores de una variable de un punto central. Estamos mirando la dispersión de los datos respecto a su centro.
las medidas de posición señalan en qué “lugar” de una distribución se encuentra un dato o un conjunto de datos en relación al resto.
En R existen distintas formas de calcular este tipo de estadísticos descriptivos.
a) Con summary
Podemos obtener rapidamente un resumen de los datos con la funcion summary de R
summary(proc_data$conf_inst) Min. 1st Qu. Median Mean 3rd Qu. Max. NA's
0.00 0.00 2.00 2.42 4.00 12.00 38 summary(proc_data$edad) Min. 1st Qu. Median Mean 3rd Qu. Max.
18.00 30.00 43.00 44.49 58.00 89.00 Con esto podemos ver que el promedio o media aritmética de la confianza en instituciones de los/as entrevistados de nuestra base es de 2.42, mientras que la mediana es de 2.
Asimismo, observamos que el 25% de la parte inferior de nuestros datos confía nada en las instituciones, en tanto que el 25% superior de la distribución de los datos confía ‘4’ en las instituciones.
Sin embargo, aunque es informativo, no nos entrega toda la información que quisiéramos.
b) Con psych
psych::describe(proc_data$conf_inst,
quant = c(.25,.75),
IQR = T) vars n mean sd median trimmed mad min max range skew kurtosis se IQR
X1 1 1162 2.42 2.49 2 2.07 2.97 0 12 12 0.88 -0.01 0.07 4
Q0.25 Q0.75
X1 0 4Usando la funcion describe del paquete psych podemos obtener mayor cantidad de estadísticos, además de especificarle otros adicionales.
Así, por ejemplo, ahora además de la media aritmética y la media, también tenemos la media recortada.
Pero lo más relevante es que nos aporta estadísticos de la dispersión de los datos, como la desviación estándar que nos indica que el grado de dispersión de mis datos respecto al promedio de confianza es de 2,49. Con esto, podemos obtener también la varianza de los datos, que corresponde a la DS al cuadrado.
Además de eso, nos aporta el rango (el valor máximo menos el mínimo), y el recorrido interquartilico (Q3 - Q1) que nos indica el grado de dispersión del 50% de los datos.
Con esta información, podemos calcular los demás estadísticos que necesitamos “a mano”, es decir, computándolos directamente en R como una calculadora.
c) Con summarise de dplyr
Otra manera de obtener todos los estadísticos que necesitamos es utilizando dplyr. Aquí, le especificamos lo que requerimos, pero debemos saber bien cómo calcular tales medidas:
proc_data %>% na.omit() %>%
summarise(media = mean(conf_inst),
mediana = median(conf_inst),
q1 = quantile(conf_inst, probs = .25),
q2 = quantile(conf_inst, probs = .75),
rango = max(conf_inst) - min(conf_inst),
desviacion_estandar = sd(conf_inst),
varianza = var(conf_inst),
coef_variacion = sd(conf_inst)/mean(conf_inst)) media mediana q1 q2 rango desviacion_estandar varianza coef_variacion
1 2.419966 2 0 4 12 2.488744 6.193847 1.028421Ahora, conocemos no solo los estádisticos anteriores, sino que también obtuvimos la varianza y el coeficiente de variación.
Resumen
Hoy aprendimos a procesar datos en R. En detalle, vimos:
Cómo establecer un flujo de trabajo de procesamiento y análisis de datos en R.
Realizar análisis descriptivos en R según el nivel de medición de las variables